Per Capita Consumption of All Cheese in the United States Per Year from 1970 to 2008

Below you will see a study that I did for my AP Statistics class that is directly correlated to this study of cheese. While we have explored the science and art of cheese in depth, now we will look at an economic outlook of fromage.

In the table below you will find the set of data being analyzed in this study.

Per  Capita Consumption of All Cheese - US
Year	Value
1970	11.3678
1971	12.0292
1972	13.0017
1973	13.4869
1974	14.407
1975	14.2703
1976	15.5113
1977	15.9917
1978	16.834
1979	17.1602
1980	17.5298
1981	18.1766
1982	19.902
1983	20.567
1984	21.4768
1985	22.5441
1986	23.1165
1987	24.0976
1988	23.7123
1989	23.793
1990	24.611
1991	24.9356
1992	25.855
1993	26.0283
1994	26.5491
1995	26.9136
1996	27.3115
1997	27.5218
1998	27.7493
1999	28.9516
2000	29.8011
2001	30.0414
2002	30.515
2003	30.5571
2004	31.2812
2005	31.7599
2006	32.6984
2007	33.1873
2008	32.4838

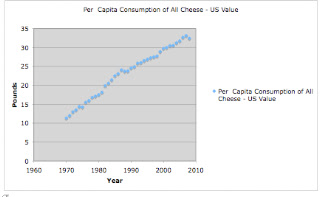
This report is a statistical analysis of the Per Capita Consumption of All Cheese in the United States each year from 1970 to 2008. The amount of consumption per person of cheese is measured in pounds. The explanatory variable (x) of time (year) is graphed versus the response variable (y) of pounds of consumption on the scatter plot below.

As made apparent by the graph, since 1970, the amount of consumption of cheese per capita has continued to rise in a positive direction with a minimum consumption of 11.3678 pounds in 1970 and a maximum of 33.1873 pounds in 2007. The scatter has a positive direction and slope, with a fairly linear shape. The plot is also very strong with an r value of .9926672127 which represents an almost perfectly linear graph (a perfect one being where r=1.)

From the data and this graph we can record the Five Number Summary of the data which is:

            Min=11.3678

            Q1=17.1602

            Median=24.0976

            Q3=28.9516

            Max=33.1873

From the five number summary, we can conclude that the IQR of the data for Pounds of Consumption= 11.7914. The data also has a range of 21.8195. There are no clear outliers in the data, so using the range would be fine for this example. The mean and median are very close in the data as well showing that the range would be fine to use. The mean= 23.2750718. Also, the standard deviation from the mean of around 23.28 is 6.559931092.

Below is a picture of the LSRL (Least Squares Regression Line) of the data. 

From this line as well as the Residual Plot (see below), it is evident that the straight-line LSRL model is the best fitting model for this group of data.

The Residual Plot pictured above has no clear pattern, further proving that the LSRL model is the best fitting one for the data.

In order to predict future values of Per Capita Consumption of All Cheese per year as well as to interpret the actual value of a point versus its predicted value by the LSRL, you can use the equation:

Y[hat] (pounds)= a+b (year)

            Where…

                        a=11.85256896

                        b=.5711251417

Also, according to the value of r² in accordance with this data, the LSRL properly accounts for 98.54% of the data. 

Overall, the data represented for the Per Capita Consumption of All Types of Cheese in the United States each year from 1970 to 2008, is a fairly linear set of data that seems like it will continue in a positive direction for upcoming years. However, as with any form of extrapolation, it is dangerous to predict too far in advanced because we do not know when this data will plateau or go down due to a lurking variable that we may not recognize at this time.